Chaos Theory: A Unpredictable World of Mathematics and Physics
Introduction to Chaos Theory
Chaos theory is a fascinating field of study that explores how systems, which might seem random and unpredictable, are actually governed by underlying patterns and rules. At its heart, chaos theory deals with deterministic systems—systems where future behavior is determined by their initial conditions, yet their outcomes are highly sensitive to small changes. This sensitivity is famously called the butterfly effect, where a tiny event, like a butterfly flapping its wings, could potentially cause a tornado in a distant place.
In both mathematics and physics, chaos theory shows how even simple systems can evolve into something incredibly complex and unpredictable over time. This randomness, however, is not due to chance but is a result of the system's complex dynamics.
Chaos Theory in Mathematics
Mathematically, chaos theory is rooted in non-linear equations, which are equations that do not form straight lines when graphed. Unlike linear systems, where small changes lead to proportional outcomes, non-linear systems can produce wildly different outcomes based on even the smallest differences in their starting points. A well-known example of a chaotic system is the logistic map, a mathematical formula used to describe population growth. The logistic map is expressed as:
Here:
- is the population at time ,
- is a growth rate constant,
- is the population at the next time step.
This equation looks simple, but for certain values of , the system becomes chaotic. Even a tiny change in the initial population can lead to drastically different future outcomes.
Chaos Theory in Physics
In physics, chaos theory appears in systems that are deterministic but unpredictable. One of the most famous chaotic systems is weather. Weather systems are governed by the laws of physics, yet we find it difficult to predict the weather accurately for more than a few days. This is because the system is highly sensitive to its initial conditions—a small difference in atmospheric conditions can lead to entirely different weather patterns.
Another example is the double pendulum. While a single pendulum swings back and forth in a predictable way, attaching a second pendulum to the first creates a system where the motion becomes unpredictable and chaotic, despite both pendulums being governed by Newton's laws of motion.
Hypotheses and Experiments in Chaos Theory
One of the key hypotheses in chaos theory is the idea that chaos is deterministic, not random. This means that, in theory, if we had perfect information about the initial conditions of a chaotic system, we could predict its future behavior. However, in practice, it is almost impossible to measure initial conditions with perfect accuracy, and even tiny inaccuracies grow over time, making long-term prediction impossible.
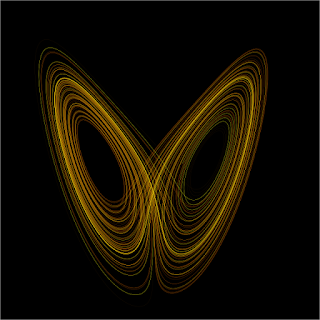
Edward Lorenz, a meteorologist, conducted one of the most famous experiments related to chaos theory in the 1960s. He was using a simple computer model to simulate weather patterns. One day, he tried to repeat a simulation but entered the initial conditions with slightly less precision. Instead of getting the same result, the weather pattern diverged dramatically, illustrating what we now call the Lorenz attractor and the butterfly effect. Lorenz's work showed that even systems governed by deterministic laws could behave unpredictably.
In terms of experiments, chaos theory can be seen in everyday life. The motion of fluids, the growth of populations, and the swings of financial markets all exhibit chaotic behavior. These systems follow mathematical rules, but predicting their behavior over long periods is impossible due to their extreme sensitivity to initial conditions.
Mathematical Expressions in Chaos Theory
Many systems in chaos theory are described using differential equations, which involve rates of change. One of the simplest examples is the Rossler attractor, a system of three linked equations that describe how a point moves through space in a chaotic way. The equations are:
Here, , , and are constants. Despite the simplicity of these equations, the behavior of the system is incredibly complex and chaotic for certain values of these constants.
Another famous set of chaotic equations is the Lorenz equations:
These equations describe the flow of fluids (like air in the atmosphere) and produce chaotic behavior when certain conditions are met.
Fun Facts and Curious Insights
Fractals and Chaos: Chaotic systems often produce patterns called fractals. A fractal is a complex structure that looks the same at different scales. For example, the shape of a coastline is fractal-like: it appears jagged whether viewed from space or up close. Fractals are a visual representation of the infinite complexity of chaotic systems.
Chaos in Nature: Chaos theory isn’t limited to mathematics or physics. It is also present in biological systems. The rhythms of the heart, for example, can sometimes exhibit chaotic behavior, which can lead to arrhythmia.
The Butterfly Effect: The idea that small changes can lead to large, unpredictable consequences comes from chaos theory. In popular culture, this concept has been explored in movies like The Butterfly Effect and Jurassic Park, where chaos leads to unpredictable consequences.
Chaos in the Stock Market: Financial markets are another example of chaotic systems. They are influenced by countless factors, and small changes in one part of the market can lead to large and unpredictable swings in prices.
Hypotheses from Scientists
Several scientists have explored the implications of chaos theory. One hypothesis, proposed by Ilya Prigogine, is that chaos plays a role in the development of complex systems in nature, such as ecosystems and living organisms. He suggested that chaotic behavior might be necessary for the evolution of life, allowing systems to adapt to changing environments.
Another hypothesis involves the connection between chaos theory and quantum mechanics. Some researchers believe that the unpredictable behavior of subatomic particles could be described by chaotic processes, bridging the gap between classical and quantum physics.
Conclusion
Chaos theory reveals the hidden complexity in seemingly simple systems. By understanding chaos, scientists can better appreciate the unpredictable nature of the world around us, from weather patterns to stock markets and beyond. While chaos might seem like randomness, it is actually a rich and intricate system governed by precise mathematical rules. The beauty of chaos lies in its unpredictability and the way small changes can ripple across a system, producing complex and often surprising outcomes.
References
- Edward Lorenz's work on the Lorenz attractor and the butterfly effect.
- Research on the logistic map and population dynamics.
- Studies of chaotic systems like the double pendulum and weather forecasting.
- Mathematical exploration of the Rossler and Lorenz attractors.
- Ilya Prigogine’s hypotheses on chaos and complex systems.
Chaos theory challenges us to think about the unpredictable side of nature, but it also opens up new ways of understanding the systems that influence our world.

No comments:
Post a Comment
Thank You for your Comments